+7 (904) 553-22-16

МЕТОД АНАЛИЗА ИЕРАРХИЙ
КАК СОСТАВНАЯ ЧАСТЬ МЕТОДОЛОГИИ
ПРОВЕДЕНИЯ ОЦЕНКИ НЕДВИЖИМОСТИ

О. А. Ахметов, М. Б. Мжельский
ООО «Сибирский Центр Оценки» г. Новосибирск

Статья опубликована в издании "Актуальные вопросы оценочной деятельности" за 2001 г.

Оценщику достаточно часто сознательно или подсознательно приходится пользоваться методами, предназначенными для проведения экспертного анализа. Поэтому в специальной литературе периодически появляются публикации, ставящие пред собой цель познакомить оценщиков с методами экспертного анализа, применимых в их практической деятельности. В частности этому посвящена статья Г.Г. Азгальдова «Проблема согласования оценок и ее возможное решение» (журнал ВОПРОСЫ ОЦЕНКИ №4’99), а также комментарий к этой статье В.А. Шакина опубликованный там же. О важности и злободневности проблемы обеспечения оценщиков соответствующим инструментарием говорит также поднятый в этих статьях вопрос о приоритетности разработанных принципов экспертного анализа, чему в статье Азгальдова уделено достаточно много внимания. Мы ни в коем случае не собираемся вдаваться в полемику по поводу приоритетов, хочется лишь отметить, что спор о приоритете разработки основ математического анализа (между Ньютоном и Лейбницем) ко всеобщему удовольствию разрешился, в конце концов мирно: были признаны заслуги обоих великих математиков и, как следствие, появился интеграл Ньютона-Лейбница.

Таким образом, на наш взгляд, необходимо в первую очередь снабдить практикующих оценщиков различными методами проведения экспертных оценок, нашедшими применение в других областях деятельности и подтвердивших свою эффективность. Как раз таким методом и является метод анализа иерархий (МАИ), разработанный Т. Саати.

Предварительная информация о МАИ

Метод анализа иерархий является систематической процедурой для иерархического представления элементов, определяющих суть проблемы. Метод состоит в декомпозиции проблемы на все более простые составляющие части и дальнейшей обработке последовательности суждений лица, принимающего решения, по парным сравнениям. В результате может быть выражена относительная степень (интенсивность) взаимодействия элементов в иерархии. Эти суждения затем выражаются численно. МАИ включает в себя процедуры синтеза множественных суждений, получения приоритетности критериев и нахождения альтернативных решений. Такой подход к решению проблемы выбора исходит из естественной способности людей думать логически и творчески, определять события и устанавливать отношения между ними.

Список применений метода весьма разнообразен: исследования транспортной системы Судана, пивоваренная промышленность Мексики, проведение анализа «стоимость-эффективность», распределение ресурсов. В Израиле профессор Ами Арбель нашел метод полезным при принятии решений как по формализуемым, так и неформализуемым факторам, для которых отсутствовали связывающие их аналитические зависимости. Метод постоянно используется при планировании промышленности Питтсбурга, банковского дела, сталелитейной промышленности, в сфере городского хозяйства и координации общественных услуг. Кроме того, необходимо отметить, что и в России этот метод получает все большее распространение: различные виды маркетинговых исследований, определение сценариев развития города, оценки различных коммерческих рисков и т.д. Во многих Вузах России, имеющих экономические специальности, вводятся соответствующие дисциплины.
Все методологии исследований различных рынков и, в частности, рынка недвижимости расположены на границе между объективной, неоднозначной, расплывчатой информацией и применяемыми четкими, жесткими методами обработки. В результате, становится необходимым соответствующий язык для перевода изучаемых проблем рынка в приемлемый для используемых методов обработки информации вид.
Роль подобного языка в МАИ выполняют различные иерархические структуры. Соответственно, в МАИ любая задача или проблема предварительно структурируются и представляются в виде иерархии древовидной или сетевой.
Таким образом, в МАИ основная цель исследования и все факторы, в той или иной степени влияющие на достижение цели, распределяются по уровням в зависимости от степени и характера влияния.
На первом уровне иерархии всегда находится одна вершина – цель проводимого исследования.
Второй уровень иерархии составляют факторы, непосредственно влияющие на достижение цели. При этом каждый фактор представляется в строящейся иерархии вершиной, соединенной с вершиной 1-го уровня. Третий уровень составляют факторы, от которых зависят вершины 2-го уровня. И так далее. Этот процесс построения иерархии продолжается до тех, пока в иерархию не включены все основные факторы или хотя бы для одного из факторов последнего уровня невозможно непосредственно получить необходимую информацию.
По окончании построения иерархии для каждой материнской вершины проводится оценка весовых коэффициентов, определяющих степень ее зависимости от влияющих на нее вершин более низкого уровня. При этом используется метод попарных сравнений.

Метод парных сравнений (версия Т. Саати).

Рассматриваемая модификация предназначена для определения структуры изучаемого объекта. Опишем метод парных сравнений (точнее модификацию по Т. Саати).
В данной модификации, как и в классическом варианте метода парных сравнений, производится сравнение изучаемых факторов между собой. Причем в данном методе факторы сравниваются попарно по отношению к их воздействию («весу», или «интенсивности») на общую для них характеристику.
Пусть в конкретной задаче необходимо определить состав некоторого объекта. Причем пусть A1, A2, ...,An основные факторы, определяющие состав объекта. Тогда для определения структуры объекта заполняется матрица парных сравнений.

	A1	A2	...	An
A1	1	a12		a1n
A2	a21	1		a2n
...			...
An	an1	an2		1

Если обозначить долю фактора Ai через wi, то элемент матрицы aij= wi/ wj.
Таким образом, в предлагаемом варианте применения метода парных сравнений, определяются не величины разностей значений факторов, а их отношение. При этом очевидно aij= 1/aji. Следовательно, матрица парных сравнений в данном случае является положительно определенной, обратносимметричной матрицей, имеющей ранг равный 1.
Работа экспертов состоит в том, что, производя попарное сравнение факторов A1, ...,An эксперт заполняет таблицу парных сравнений. Важно понять, что если w1, w2, ..., wn неизвестны заранее, то попарные сравнения элементов производятся с использованием субъективных суждений, численно оцениваемых по шкале, а затем решается проблема нахождения компонента w.
В подобной постановке задачи решение проблемы состоит в отыскании вектора (w1, w2, ..., wn). Существует несколько различных способов вычисления искомого вектора. Каждый из методов позволяет кроме непосредственного нахождения вектора отвечать еще на некоторые дополнительные вопросы. Подробнее об этом будет написано ниже.
Подчеркнем, что эксперт сравнивая n факторов реально проводит не n (как это происходит при заполнении обычных анкет) сравнений, а n*(n-1)/2 сравнений. Но это еще не все. На самом деле (учитывая соотношение aij=aiк* aкj справедливое для всех значений индекса k) производится опосредованное сравнение факторов Ai и Aj через соответствующие сравнения этих факторов с фактором Ak. Принимая во внимание сделанное замечание можно утверждать, что в действительности эксперт производит значительно больше сравнений, чем даже показывает первая оценка равная n*(n-1)/2. Таким образом, каждая клетка матрицы парных сравнений реально содержит не одно число (результат непосредственного сравнения), а целый вектор (с учетом всех опосредованных сравнений через сравнения с другими факторами). Учет этих дополнительных сравнений позволяет значительно повысить надежность получаемых результатов, или позволяет значительно уменьшить количество необходимых экспертов.
Один из основных методов отыскания вектора w основывается на одном из утверждений линейной алгебры.
Очевидно, что искомый вектор является собственным вектором матрицы парных сравнений, соответствующим максимальному собственному числу (lmax). В этом случае по одному из большого количества существующих алгоритмов max, а затем достаточно решить векторное уравнение A*w=lотыскивается lmax*w.
Здесь необходимо отметить следующее. Из линейной алгебры известно, что у положительно определенной, обратносимметричной матрицы, имеющей ранг равный 1, максимальное собственное число равно размерности этой матрицы (т.е. n). При проведении сравнений в реальной ситуации вычисленное максимальное собственное число lmax будет отличаться от соответствующего собственного числа для идеальной матрицы. Это различие характеризует так называемую рассогласованность реальной матрицы. И, соответственно, характеризует уровень доверия к полученным результатам. Чем больше это отличие, тем меньше доверие. Таким образом, эта модификация метода парных сравнений содержит внутренние инструменты позволяющие определить качество обрабатываемых данных и степень доверия к ним. Эта особенность данной методики выгодно отличает его от большинства обычно применяемых при исследовании рынка методов.
Другой подход в определении вектора w состоит в следующем. Суммируются по строкам элементы матрицы парных сравнений (для каждого значения i вычисляется сумма ai=ai1+ ai2+...+ ain). Затем все ai нормируются так, чтобы их сумма была равна 1. В результате получаем искомый вектор w. Таким образом
wi=ai/(a1+ a2+...+ an).
Этот способ нахождения вектора w, значительно проще в реализации, но он не позволяет определять качество исходных данных.
Приведенное выше описание метода является разработкой собственно Т. Саати и его группы. При всех его достоинствах данная версия не лишена некоторых недостатков. На этих недостатках мы и остановимся.
Как уже отмечалось, рассматриваемая версия метода парных сравнений, позволяет определить качество исходных данных. Причем Саати рекомендует при плохо согласованной матрице либо сменить экспертов, либо найти дополнительные данные, либо решать проблему другим методом. Эта возможность является серьезным достоинством данного метода, но на наш взгляд в некоторых случаях данное преимущество переходит в свою противоположность. В том случае, когда проблема не в экспертах, а в собственно объекте изучения. Рассогласованность матрицы парных сравнений может быть вызвана, по крайней мере двумя факторами:
(а) личными качествами эксперта;
(б) степенью неопределенности объекта оценки.
Поэтому рассогласованность матрицы выступает как результат взаимодействия этих факторов. И, следовательно, игнорирование такой структуры причин рассогласования приводит к тому, что рекомендуемые мероприятия по повышению согласованности матрицы проводятся не только в ситуациях, когда большая рассогласованность является следствием низкой профессиональности эксперта, но и в случаях, когда подобная неоднозначность является неотъемлемой частью изучаемого объекта, что, как правило, и происходит при изучении рынка недвижимости. В последнем случае необходимо изучать объект такой, какой он есть со всеми присущими ему неопределенностями.
Для того, чтобы выделить ту составляющую рассогласованности, которая определяется собственно экспертом, необходимо несколько изменить взгляд на объект и на ожидаемый результат обработки исходных данных.
Прежде всего, необходимо признать, что объекту исследования (в частности, рынку) присуща некоторая неопределенность. И, как следствие, ожидать однозначного результата было бы не разумно. Ответ может и должен быть сформулирован на языке вероятности, т.е. либо в виде доверительных интервалов, либо в виде вероятности реализации интересующего результата, либо в виде математического ожидания результата и его дисперсии и т.д.
Построить алгоритм обработки матрицы сравнений, представляющий результаты в необходимой форме, позволяет отмеченное выше свойство матрицы сравнений: каждый элемент матрицы является, по сути, целым вектором, составленным из различных сравнений (прямых и опосредованных) соответствующих факторов. Учитывая это свойство можно для каждого элемента матрицы сопоставить его среднее значение и его стандартное квадратичное отклонение (СКО). Далее пользуясь методами стохастического моделирования можно построить последовательности матриц сравнения, каждая из которых будет соответствовать одной из возможных реализаций отношений характерных для данного объекта в рамках его неоднозначности и компетентности оценивающих его экспертов. Определяя для каждой такой матрицы вектор w, получим достаточно большой набор векторов, представляющих возможные реализации структуры объекта в соответствии с его неоднозначностью и компетентностью оценивающих его экспертов. Воспринимая, построенный подобным образом, набор векторов, как статистическую выборку, можно получить необходимый результат в том виде, который необходим в конкретном случае. В частности легко можно получить средние значения компонент вектора w и значения их СКО.
Полученные таким образом значения СКО и являются следствием степени рассогласованности матрицы парных сравнений. Чем больше рассогласованность, тем больше значения СКО.
Казалось бы, что для того чтобы определить уровень рассогласованности не нужны подобные нагромождения, что можно обойтись способом, предложенным Т. Саати и описанным выше. Но все это нагромождение позволяет решить важную проблему, связанную с причинами возникновения этой самой рассогласованности. Дело в том, что, заполняя матрицу сравнений эксперт может заполнить ее только выше главной диагонали. Остальная ее часть рассчитывается с учетом обратной симметричности. Но если эксперт заполняет не только верхнюю, но и нижнюю часть матрицы, то появляется дополнительная информация, позволяющая оценить степень личной компетентности данного эксперта.
Действительно, при сравнении фактора Ai с фактором Aj эксперт поставит оценку aij, а при сравнении фактора Aj с фактором Ai эксперт поставит оценку aji. При этом на взаимное соотношение этих оценок не влияет состояние рынка, а только профессионализм эксперта (в идеальном случае, как уже отмечалось, должно выполняться равенство aji=1/ aij). Таким образом, отклонение aji от 1/ aij является случайной величиной и ее СКО соответствует уровню профессионализма эксперта. Следовательно, учитывая свойства дисперсии, можно из оценок элементов матрицы сравнений убрать влияние непрофессионализма эксперта и в результате уменьшить СКО компонентов вектора w. В итоге вектор w, точнее средние значения его компонент и их СКО, будет соответствовать данному объекту (в частности рынку) и адекватно описывать его.

Итак, учитывая степень неоднородности и неопределенности сложившегося рынка, можно быть уверенным, что, описанная выше новая модификация метода парных сравнений позволит получать корректные результаты при проведении рыночных исследований.
Для проведения субъективных парных сравнений Т. Саати была разработана шкала относительной важности.

Шкала относительной важности

Интенсивность относительной важности	Определение	Объяснение
0	Несравнимы	Эксперт затрудняется в сравнении
1	Равная важность	Равный вклад двух видов деятельности в цель
3	Умеренное превосходство одного над другим	Опыт и суждения дают легкое превосходство одному виду деятельности над другим
5	Существенное или сильное превосходство	Опыт и суждения дают сильное превосходство одному виду деятельности над другим
7	Значительное превосходство	Одному из видов деятельности дается настолько сильное превосходство, что оно становится практически значительным
9	Очень сильное превосходство	Очевидность превосходства одного вида деятельности над другим подтверждается наиболее сильно
2,4,6,8	Промежуточные решения между двумя соседними суждениями	Применяются в компромиссном случае
Обратные величины приведенных выше чисел	Если при сравнении одного вида деятельности с другим получено одно из вышеуказанных чисел (например, 3), то при сравнении второго вида деятельности с первым получим обратную величину (т.е. 1/3)

Выбор шкалы определялся следующими требованиями:
(а) Шкала должна давать возможность улавливать разницу в чувствах людей, когда они проводят сравнения, различать как можно больше оттенков чувств, которые имеют люди.
(б) Эксперт должен быть уверенным во всех градациях своих суждений одновременно.
Как показывают работы автора Т. Саати по сравнению этой шкалы с 28 другими шкалами, предложенными разными лицами, эта шкала и ее незначительные модификации лучше, чем все другие шкалы.
Хочется к этому лишь добавить, что данный метод парных сравнений и данная шкала чрезвычайно хорошо приспособлены к особенностям обработки информации человеком. Но при этом данная шкала не является обязательной. Как видно из приведенного краткого описания данная модификация метода безразлична к обычно используемым типам шкал.

МАИ и некоторые задачи оценки недвижимости

1. Первой рассмотрим задачу об оценке отношения спроса к предложению на рынке недвижимости. Ее решение является важным этапом при использовании затратного подхода, а также оценке земельного участка методом остатка.
Одним из подходов, позволяющих провести необходимую оценку, является непосредственная оценка, как спроса, так и предложения. Но возникающие при этом проблемы связаны с нахождением надежных исходных данных. К сожалению, в настоящее время сложно рассчитывать на получение подобной информации. И, соответственно, приходится искать опосредованные методы по определению указанного отношения.
Применение МАИ позволяет построить такую методику. И, поскольку этот метод является экспертным, постольку результат будет соответствовать конкретному изучаемому рынку недвижимости.
Построение экспертной модели по оценке отношения спроса к предложению необходимо начинать с построения иерархии. При этом, учитывая особенности МАИ, представляется более естественным оценивать сразу отношение, не разбивая его на составляющие. В этом случае в беседах с экспертами определяется список факторов, определяющих искомое отношение. В результате получим следующую иерархию:

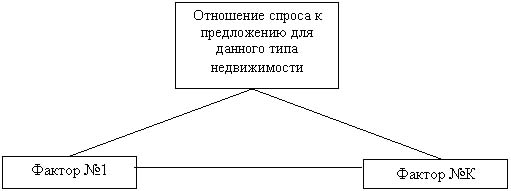
Затем с помощью метода попарных сравнений происходит определение весовых коэффициентов, соответствующих степени влияния конкретного фактора на отношение спроса к предложению. Затем для каждого фактора определяется шкала возможных значений.
В дальнейшем определяются значения всех факторов в соответствующих шкалах. Это можно сделать по крайней мере двумя способами: либо напрямую (если позволяет имеющаяся в наличии информация), либо опять же проведя среди экспертов попарное сравнение между допустимыми значениями фактора. Если же отсутствуют данные о реальных значениях факторов и эксперты затрудняются провести указанные сравнения, то необходимо провести дополнительное разбиение подобного фактора на систему субфакторов. Оценив их весовые коэффициенты и определив значения, получаем значение проблематичного фактора.
Последовательно применяя указанный способ разбиения и проводя определения весовых коэффициентов, можно построить иерархию и получить с ее помощью значение отношения спроса к предложению.
2. В качестве второго приложения МАИ рассмотрим уже обсуждавшийся (журнал «ВОПРОСЫ ОЦЕНКИ» №4 за 99 год статья Г.Г. Азгольдова «Проблема согласования оценок и ее возможное решение», а также В.А. Шакин «Комментарий к статье Г.Г. Азгольдова «Проблема согласования оценок и ее возможное решение»») вопрос о согласовании результатов оценки, полученных различными методами в рамках затратного, рыночного и доходного подходов.
На наш взгляд требование соответствия применяемого метода цели, с которой проводится оценка, является важнейшим. Но одновременно нельзя не принимать во внимание и оценки, полученные другими методами. Также нельзя не учитывать и степень надежности используемой исходной информации. В результате объединения этих требований и в соответствии с описанным подходом построим иерархию.

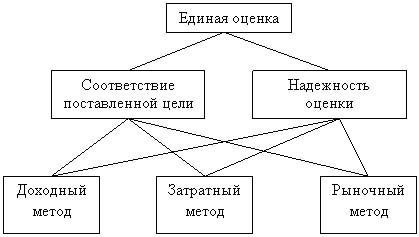
В соответствии с построенной иерархией, для получения единой оценки, прежде всего, необходимо определиться в той степени, в которой характеристики «соответствие поставленной цели» и «надежность оценки» определяют единую оценку. Совершенно ясно, что обе характеристики важны, но которая важнее и во сколько важнее необходимо определить в первую очередь. Для этого наряду с другими подходами можно воспользоваться и методом попарных сравнений. Для этого заполним матрицу парных сравнений:

	Соответствие	Надежность
Соответствие	1	7
Надежность	1/7	1

Такое задание степени предпочтения характеристики «соответствие» перед характеристикой «надежность» определяет следующие весовые коэффициенты:
• «соответствие» – 0,875;
• «надежность» - 0,125.
На следующем этапе определяем, какой из применяемых методов проведения оценки наиболее соответствует цели. Для этого формируется соответствующая матрица парных сравнений:

	Затратный	Рыночный	Доходный
Затратный	1	1/5	1/3
Рыночный	5	1	5
Доходный	3	1/5	1

Данная матрица показывает, что рыночный подход наиболее соответствует цели проведения данной оценки, несколько в меньшей степени этой цели соответствует доходный метод и совсем мало соответствует затратный подход. Соответствующие весовые коэффициенты (в порядке, определяемом матрицей) равны: 0,083; 0,564; 0,353.

Аналогичная матрица для определения степени надежности оценок (в соответствии со статьей Г.Г. Азгальдова) имеет вид

	Затратный	Рыночный	Доходный
Затратный	1	0,6	0,85
Рыночный	1,67	1	1,43
Доходный	1,17	0,7	1

Соответствующие весовые коэффициенты для характеристики «надежность» будут равны: 0,26; 0,43; 0,31.
Следуя примеру приведенному Г.Г. Азгальдовым примем значение стоимости недвижимости по затратному методу равное 1550000 руб., по рыночному методу – 1240000 руб. и, наконец, по доходному методу – 1880000 руб.
Тогда с учетом весовых коэффициентов получаем объединенную оценку данной недвижимости равную 1519000 руб.
Постольку поскольку рыночный подход наиболее соответствует цели проведения оценки и этот же метод является наиболее надежным, то естественно и итоговая оценка в большей степени определяется рыночным подходом.
Если же матрица, описывающая сравнения характеристик по степени их соответствия цели, будет иная:

	Затратный	Рыночный	Доходный
Затратный	1	1/5	1/7
Рыночный	5	1	1/2
Доходный	7	2	1

 

Метод анализа иерархий Часть 2